How to Find Rate of Change of a Graphed Function

There are various ways to determine the rate of change of a graphed function. One way to do this is by finding the average rate of change. Another option is to use a calculator to find the rate of change. You may also use a nonlinear function to find the rate of change.

Introduction of Average rate of change

Average rate of change can be used to calculate the slope of a graphed function. It is defined as the rate of change of one quantity with respect to another quantity. This rate can be obtained by comparing pairs of input and output values.

For a linear function, the average rate of change will always be the same. However, this is not the case for nonlinear functions. They will have a different slope depending on the points used in the equation.

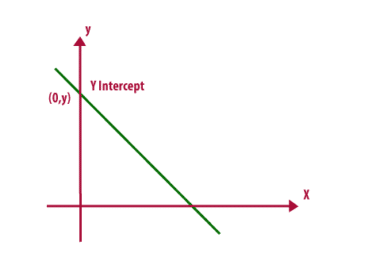
The average rate of change of a linear function can be expressed as the slope of the line connecting the endpoints of an interval. This line will have a gradient of 1 for both quantities. In other words, when the line is cut between the two points, the average rate of change of the function is zero.

Similarly, the average rate of change of a function between two points can be derived by drawing a line between the two points. When the line is a straight line, the gradient is equal to 1 for both the x and y coordinates. On the other hand, if the line is a secant line, the slope will be the average rate of change.

An example of the average rate of change of a function is the increase in the number of fish in a lake. If the fish numbers are 100 in a week, the average rate of change of the function would be 5. Another example is the increase in speed. A bus travels at 80 km per hour.

How can you find the rate of change of a graphed function

How can you find the rate of change of a graphed function? A graphed function is a linear or nonlinear function that shows the relationship between the output and input values. The rate of change is the change in the y-values of the function on a given interval.

Rate of change is an essential characteristic of functions. It is visible in equations and tables, but can also be seen in graphs. It is the change in one value as a result of a change in another. As the output value increases, the input value is expected to decrease. In other words, an increasing function will go from left to right. However, an increasing function’s rate of change is positive. On the other hand, a decreasing function will have a negative rate of change.

When a function is graphed, it is usually done using a set of random values for x and y. Care should be taken to avoid asymptotes, and the range should be kept consistent. You should also expect to see a local maximum or minimum at some point in the graph. Most graphing calculators can estimate the location of a function’s minimum or maximum.

Average rate of change is a method of calculating the slope of a graphed function. This can be determined by identifying points on the graph and calculating the change between these points. The formula for the average rate of change is y = mx+b where m is the slope and b is the intercept. Using this formula, you can find the average rate of change of any graphed function.

Non-linear function

A non-linear function is a function that has a graph other than a straight line. These functions include logarithmic, exponential and trigonometric functions. They can be represented in several ways, including graphs, tables and equations.

One of the most important concepts in calculus is the average rate of change. This concept provides a means of calculating the rate at which the output of a function changes relative to the input. It is useful in determining how fast the output of a non-linear function is changing compared to the input. The formula for average rate of change involves dividing the change in the y-values of the function by the change in the x-values of the function.

The equation for a nonlinear function is f(x) = ax + b. In this case, x is the independent variable and b is the dependent variable. To find the rate of change of this function, the graph of the function must be determined.

Linear functions are defined in a table and have a graph on the coordinate plane. They have an initial value called the y-intercept. When the point of evaluation changes, the slope of the function changes. As the point of evaluation increases, the slope of the function goes up. On the other hand, when the point of evaluation decreases, the slope goes down.

Calculator

If you’re working on a problem where you need to find the rate of change, you can use a calculator. This can help you get an answer without having to think too hard. However, the algorithm used by this tool may not always work properly. You’ll need to check and test the results to make sure they are accurate.

A rate of change is the change in the value of a function with respect to an independent variable. It is a measure of how well a quantity changes over time. The formula for calculating a rate of change can be applied to any function. There are two ways to calculate a rate of change: a positive and a negative.

For a positive rate of change, the change in the x-value will cause the y-value to decrease. On the other hand, a negative rate of change will result in a downward slanting graph.

Read Also: How To Use Sohcahtoa?

In order to use an average rate of change calculator, you’ll need to enter your input values. These values should be the y and x values of a function that is based on a tangent line. Once you enter these numbers, the calculator will calculate the average rate of change for the input values.

When you are finished entering your values, you’ll be prompted to provide feedback to the program. If you’ve entered a wrong input or there is an error, the program will tell you.

After you have finished completing the input process, you’ll be taken to a second window where you can see the resulting instantaneous rate of change. Here you’ll need to enter a value for x and an instant for which the rate of change is needed.