Implicit differentiation calculator: The calculator over discovers the value of your derivative order input by using the process known as implied differentiation. It makes use of comparable actions to conventional paper and also pencil Calculus, but much faster than what a human is capable of.
Using implied differentiation to calculate a by-product serves when the reliant variable not isolated on one side of the formula (typically y is the dependent variable). When the reliant variable is on the same side of the equation as the independent variable and cannot be subtracted or included in the opposite to isolate it, implicit differentiation is needed.
Read Also: What Are Agents of Socialization?
A formula like such is called an implicit relationship since one variable is an implicit function of the other variable. Let’s take a look at an example of an implicit relationship (XY) = 2. If we intended to compute the derivative dy ⁄ dx of this equation, we are incapable of using the normal trigonometry acquired policies to distinguish the wrong term with x since that term also has y in it.
The necessary procedure for implied differentiation is to take the derivative of both sides of the equation, and after that, isolate the complete differential operator. For example, in the event where the equation has y as the reliant variable as well as x as the independent variable, we would undoubtedly take d ⁄ dx of both sides of the equation, and after that function to isolate dy ⁄ dx. When dy ⁄ dx is separated, we have the final, streamlined kind of the set-apart function.
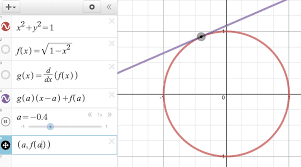
Implicit differentiation calculator
As much as this point in calculus, many features acquired remained in explicit form.
Explicit form is the basic y = 2x + 5 or any other feature where y gets on one side of the equal sign as well as x is on the other.
Implicit Features are different, in that x and y can be on the same side.
A straightforward example is: XY = 1. It is here to use the implied distinction.
Bear in mind. You have used all of these acquired rules before. Y isolated for you.
An implicit kind of a formula of 2 variables is an equation where both variables are non-linear, so we cannot get a specific type, where we write one variable in regard to the other.
For instance, the formula of a circle in a rectangular formula provided as a formula where both variables appear squared, so it cannot be composed explicitly as a single formula.
The implicit distinction is the process of differentiation of an implied kind, where we make use of the Chain guideline since the two variables are not straight.
Applications
Presuming you are flying a kite that keeps a consistent elevation of 40 meters and also the kite string is a straight line. If you are going to the right with 1 meter per second and the kite string is extending at 1 meter per 2nd, to locate the horizontal rate of the kite at the split second when the kite is 30 meters behind you, do the complying with actions.
Read Also: What Is Removable Discontinuity?
1) Represent the string variation with x as well as the horizontal displacement of the kite with y. Acquire a partnership between x and also y utilizing the best triangular with the hypotenuse, 50 + x, as well as the sides with an upright size of 40 and the horizontal size y + 30 + x.
2) Usage implicit differentiation to set apart the relationship in 1) and discover y.
Implicit Differentiation
Implicit differentiation is typically made use of in discovering the slope of the tangent line to a curve given up rectangle-shaped type as an implied kind or in relevant rates problems.
In associated price trouble, we gave a rate of change of a variable. Also, we require to locate the rate of adjustment of an additional variable.
For this, we require to do the adhering to two steps:
- figure out a partnership between the two variables, which usually is an implied form
- use the implicit distinction to locate a connection between the two prices and also address the unknown price.
Implicit Differentiation Strategy
Let’s say that our buddy Gary is letting us recognize that he’s most likely to be late for our 4:15 PM supper meeting, yet all he states is that there’s still lots of homework that he has to do. When asked to be more transparent, Gary explicitly shares his schedule: at 4 PM, he examines math. At 4:10, he pauses, and also at 4:20. He begins the homework. By explicitly stating his routine, we understand for certain Gary has no plans to be at the restaurant by 4:15.
Read Also: Spanish Verb Seguir Conjugation
In mathematics distinction troubles, we frequently listen to these very same words: specific and implied. In this lesson, we clarify the implicit distinction method by contrasting it to particular differentiation. We, after that, complete several examples utilizing implicit differentiation. This may aid Gary to make it to the restaurant.
Final Words
Differential calculus is the research study of the rates at which quantities adjustments. The key objects of study in differential calculus are the by-products of a function, associated ideas such as the differential, and also their applications. The derivative of a feature describes the rate of modification of features near the input value—the manufacturer of locating the derivative called distinction. Now, Implied features are those functions in mathematics in which the dependent variable has not been offered explicitly regarding the independent variable. If we find the worth of x by solving an equation of the kind:
R( x, y) = 0.
While in a specific feature, a prescription given to establish the value of function y in regard to the input value x:
y = f(x ).
In implied differentiation, a regulation called chain regulation used to differentiate unconditionally specified functions. As I have described earlier on this web page, variable y can be given as a function of x implicitly instead then explicitly. In Implicit differentiation, there is no genuine difference between the appearance of x and y. All the implied equations are be reactivated explicitly in one formula.
Hope you liked this detailed article on the Implicit differentiation calculator.