How To Work With 30-60-90-degree Triangles
30 60 90 Triangle: If you’ve had any experience with geometry, you probably know that there are many different types of triangles. They can be classified by side length (isosceles, scalene, or equilateral) or by angle measurement (acute, obtuse, or right). Additionally, some of these types can be classified even further into smaller groups.
Read Also: Learn Details about 30 60 90 triangle
This lesson is going to examine one kind of right triangle, which is a triangle that has exactly one right, or 90 degree, angle. This specific kind is a 30-60-90 triangle, which is just a right triangle where the two acute angles are 30 and 60 degrees. Why does this specific triangle have a special name? Let’s find out.

What is the formula for 30 60 90 Triangle?
Divide the hypotenuse by 2 to find the short side. Multiply this answer by the square root of 3 to find the long leg. Type 3: You know the long leg (the side across from the 60-degree angle). … Double that figure to find the hypotenuse. Finding the other sides of a 30–60–90 triangle when you know the hypotenuse.
How do you solve a 30 60 90 Triangle?
It turns out that in a 30–60–90 triangle, you can find the measure of any of the three sides, simply by knowing the measure of at least one side in the triangle. The hypotenuse is equal to twice the length of the shorter leg, which is the side across from the 30 degree angle.
30 60 90 Triangle Calculator
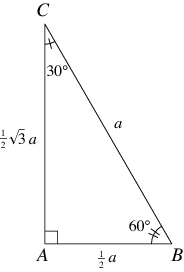
A 30-60-90 triangle is a right triangle having angles of ![]() ,
, ![]() , and
, and ![]() . For a 30-60-90 triangle with hypotenuse of length
. For a 30-60-90 triangle with hypotenuse of length ![]() , the legs have lengths
, the legs have lengths
|
(1)
|
|||
|
(2)
|
and the area is
|
(3)
|
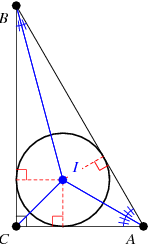 |
 |
The inradius ![]() and circumradius
and circumradius ![]() are
are
|
(4)
|
|||
|
(5)
|
The mean length of a line segment picked at random in a 30-60-90 triangle was computed by E. W. Weisstein (Aug. 5, 2010) as a complicated analytic expression involving sums of logarithms. After simplification, the result can be written as
|
(6)
|
|||
|
(7)
|
(E. Weisstein, M. Trott, A. Strzebonski, pers. comm., Aug. 25, 2010; OEIS A180308).

30-60-90 triangles are used in drafting, as illustrated above. This allows lines of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() to be drawn by sliding the drafting triangle along a T-square.
to be drawn by sliding the drafting triangle along a T-square.
30 60 90 Triangle Ratio
A 30-60-90 triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees. Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another.
The basic 30-60-90 triangle ratio is:
Side opposite the 30° angle: x
Side opposite the 60° angle: x * √3
Side opposite the 90° angle: 2x
All 30-60-90-degree triangles have sides with the same basic ratio. Two of the most common right triangles are 30-60-90 and 45-45-90 degree triangles. If you look at the 30–60–90-degree triangle in radians, it translates to the following:
![]()
In any 30-60-90 triangle, you see the following:
-
The shortest leg is across from the 30-degree angle.
-
The length of the hypotenuse is always two times the length of the shortest leg.
-
You can find the long leg by multiplying the short leg by the square root of 3.
30-60-90 Triangle Rules
How do we know that the side lengths of the 30-60-90 triangle are always in the ratio 1:3–√:2 ? While we can use a geometric proof, it’s probably more helpful to review triangle properties, since knowing these properties will help you with other geometry and trigonometry problems.
Here are a few triangle properties to be aware of:
- In any triangle, the angle measures add up to 180º. In other words, if you know the measure of two of the angles, you can find the measure of the third by subtracting the measure of the two angles from 180.
- In any triangle, the side opposite the smallest angle is always the shortest, while the side opposite the largest angle is always the longest. You can see how that applies with to the 30-60-90 triangle above.
- Triangles with the same degree measures are similar and their sides will be in the same ratio to each other. This means that all 30-60-90 triangles are similar, and we can use this information to solve problems using the similarity.
In addition, here are a few triangle properties that are specific to right triangles:
- In right triangles, the side opposite the 90º angle is called the hypotenuse, and the other two sides are the legs.
- In right triangles, the Pythagorean theorem explains the relationship between the legs and the hypotenuse: the sum of the length of each leg squared equals the length of the hypotenuse squared, or a2+b2=c2.
Based on this information, if a problem says that we have a right triangle and we’re told that one of the angles is 30º, we can use the first property listed to know that the other angle will be 60º. This is often how 30-60-90 triangles appear on standardized tests—as a right triangle with an angle measure of 30º or 60º and you are left to figure out that it’s 30-60-90.
Not only that, the right angle of a right triangle is always the largest angle—using property 1 again, the other two angles will have to add up to 90º, meaning each of them can’t be more than 90º. Since the right angle is always the largest angle, the hypotenuse is always the longest side using property 2.
We can use the Pythagorean theorem to show that the ratio of sides work with the basic 30-60-90 triangle above.
a2+b2=c2
12+(3–√)2=1+3=4=c2
4–√=2=c
Using property 3, we know that all 30-60-90 triangles are similar and their sides will be in the same ratio.