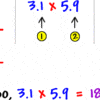
It isn’t easy to imagine how our life would certainly be without mathematical concepts such as percentages or proportion. In our daily lives, we often come across rates and proportions when choosing to purchase, cooking and when on an occupation trip, etc.
Proportions, as well as percentages, are crucial for– reliable efficiency. In this, post we will find out exactly how to compute proportions and solve sample issues. However, before that, let’s begin by defining ratios.
A ratio is a method of making contrasts between two or more amounts. The indication used to signify a proportion is colon ‘:’ Mean an, and b are two different quantities or numbers. After that, the proportion of a to b can create as a/b or a: b. Likewise, the ratio of b to a can additionally be stood for as b: a or b/a. The initial amount in a proportion is called antecedent, and the 2nd worth is referred to as the consequent.
Instances of proportions are 3/4 or 3: 4, 1/5 or 1: 5, 199/389 or 199:389 etc. From this example, a ratio is simply a fraction where the antecedent is the numerator, and the consequent is the common denominator.
The famous Vitruvian Male illustration of Leonardo da Vinci was based upon the perfect ratio of the body. Each part of the body occupies a different percentage like the face takes up about 1/10 of the total elevation, and the head uses up about 1/8 of the overall height. The writers in the middle ages used the word proportion (percentage) for the very first time. In 1948, Le Corbusier provided a system of proportions.
Table of Contents
What is a Proportion?
A proportion is an expression that tells us that two ratios are equivalent. Two proportions state to be proportional if they are equal. Percentages are stood for by the sign ‘:’ or ‘=’. For example, if a, b, c, and d are integers, the proportion is composed as a: b = c: d or a/b = c/d or b: a = d: c. For instance, the ratios 3: 5 and also 15: 25 are proportional and are written as 3: 5= 15: 25
The four numbers a, b, c and d are known as the regards to a percentage. The initial an and the last term d are described as extreme terms while the second, as well as 3rd terms in a proportional, are called mean terms.
How to Solve Ratios?
It is easy to determine if proportions are proportional. To check if the proportion a: b and also c: d is proportional.
Multiply the first with the last term: an x d.
Multiply the 2nd term with the third term: b x c.
If the product of strict terms amounts to the development of mean times, after that, the ratios are symmetrical: an x d = b x c.
Continued proportion.
Two ratios, b: c and a: b, is said to be in continued proportion if a: b = b: c. In this situation, the term c is called the 3rd proportion of an and b, whereas b is called the mean proportion of in between the terms and c.
When the terms a, b, and care in continued percentage, the complying with formula obtains.
a/b = b/c.
Cross is increasing the terms gives; an x c =b x b, Therefore.
b ² = a/c.
Example
Figure out if the list below ratios remains in percentage: 8:10 as well as 12:15.
Solution
Increase the initial and also 4th terms of the ratios.
8 × 15 = 120.
Now multiply the 2nd and also 3rd term.
10 × 12 = 120.
Because the item of the extremes amounts to the product of the ways.
Since the item of means (120) = product of extremes (120 ),.
For that reason, 8: 10 and 12:15 are symmetrical.
Golden Ratio
The most significant application of the percentage is the gold proportion, which assisted a whole lot in examining percentages of various things and synthetic systems like economic markets. Both amounts state to be in gold proportion if their ratio amounts to the ratio of their sum to the bigger of the two quantities, i.e. (a + b)/ a = a/b, where a > b > 0.
This proportion represents by the Greek letter φ. More simplifying this formula, we get, φ 2– φ– 1 = 0. And also, fixing this by making use of a square formula, we obtain φ = 1.6180339887 …
Euclid and lots of mathematicians worked with the golden ratio and found its presence in the regular pentagon and gold rectangular shape.