What are skew lines? How do we recognize a pair of skew lines? Let’s begin with a short definition of skew lines:
These lines are two or even more lines that are not: intersecting, parallel, and also coplanar to each other.
Identical Lines– these are lines that rest on the very same aircraft but never meet.
Converging Lines— these are lines that rest on the very same aircraft as well as fulfil.
Coplanar Lines— these are lines that push the same plane.
In this article, you will undoubtedly discover what lines are, how to learn skew, and establish whether two offered lines are skewed.
More about skew lines
They are two or more lines that do not intersect. Also, they are not parallel and are not coplanar. (Keep in mind that parallel lines and intersecting lines push the very same aircraft.).
This makes lines unique– you can only locate lines in figures with three or even more dimensions.
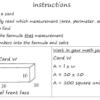
The lines as well as are examples of 2 skew for every number. You can recognize right away by seeing how they lie on various surface areas and positioned to ensure that they are not parallel or intersecting.
What are real-world examples?
Since skew lines discover in 3 or even more measurements, our world will contain lines. Below are some examples to aid you in much better visualize skew lines.
The lines located on the walls as well as the ceiling’s corresponding surfaces.
Because the lines on each of the surface areas are in different planes, the lines within each of the surface areas will never meet, nor will certainly they be parallel.
Two or even more road indications are lying along with the same post.
The lines in each street indication are not in the same aircraft and intersecting or alongside each other.
Roadways along freeways and also overpasses in a city.
Given that the roads are considered separate planes, lines found in each will never intersect or are alongside each other.
How to find skew lines?
When offered a figure or real-world instances, to locate a pair of lines, always return to the meaning of skew lines. Ask the adhering to concerns.
What are the lines (in the number) that do not converge with each other?
Are the selected lines not located lying on the same aeroplane?
Are the chosen lines not parallel per various others?
If the solution to the three concerns is YES, you have located a set of two lines.
In the cube revealed, as well as are examples of two lines that are skewed. You can validate this by inspecting the problems for changing lines.
And do not intersect.
As well as do not rest on the very same plane.
And are not parallel.
This verifies that the two are skew concerning each other.
What are other skew lines’ interpretations?
We have reviewed just how to find skew lines from figures in the previous sections. Currently, we can take a quick look right into an additional meaning of lines in more excellent mathematics.
The lines only when it is not equal to absolutely no.
We will not use this interpretation of skewed lines in a precalculus class, so in the meantime, we can check out the formulas briefly and also focus on the geometric idea of lines.
Example
Which of the following figures will you have the ability to discover lines?
Hexagon.
Dice.
The surface area of a Round.
Octagon.
Solution.
By theory, we can only find lines in numbers with three or even more dimensions. Aeroplanes can never consist of lines, so (a), (c), and (d) are no more legitimate options.
Dices are three-dimensional and can consist of lines. So, it’s b.