What Is Removable Discontinuity?
Removable Discontinuity: A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. There is a gap at that location when you are looking at the graph. When graphed, it is marked by an open circle on the graph at the point where the graph is undefined or is a different value like this.
There are two ways the graph can be created. Let’s talk about the first one now. Do you see it? There is a small open circle at the point where x=2.5 approximately.
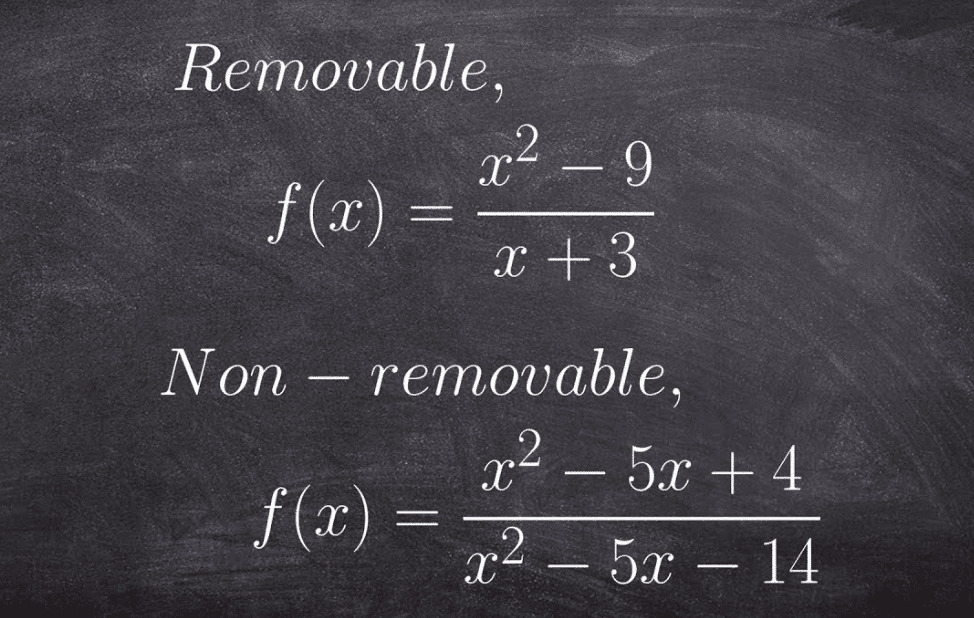
A hole in a graph. That is a discontinuity that can be “repaired” by filling in a single point. In other words, a removable discontinuity is a point at which a graph is not connected but can be made connected by filling in a single point.
Read Also: Parent Functions And Transformations
Formally, a removable discontinuity is one at which the limit of the function exists but does not equal the value of the function at that point; this may be because the function does not exist at that point.
How Do You Solve A Removable Discontinuity?
To solve a removable discontinuity, also known as a hole in the graph, you can follow these steps:
- Identify the point of discontinuity. This is the point where the graph has a hole.
- Factor the expression that represents the function. For example, if the function is f(x) = (x^2 – 4)/(x – 2), you can factor it as f(x) = (x + 2)(x – 2)/(x – 2).
- Simplify the expression by canceling out the common factor in the numerator and denominator. In the example above, you can cancel out the (x – 2) factor to get f(x) = x + 2.
- Check the simplified expression for any values that make the denominator equal to zero, as these values are not in the domain of the function. In the example above, the value x = 2 makes the denominator equal to zero, which means that x = 2 is not in the domain of the function.
- Replace the removed value in the simplified expression to create a new function that fills in the hole. In the example above, you can replace x = 2 in f(x) = x + 2 to get f(x) = 4.
- Graph the new function to show the removed value has been filled in. The graph should have a continuous curve without any holes or gaps.
By following these steps, you can solve a removable discontinuity and create a new function that is continuous over the point of discontinuity.
What Is The Difference Between A Removable And Non-Removable Discontinuity?
Removable And Non-removable Discontinuity
As your pre-calculus teacher will tell you, functions that aren’t continuous at an x value either have a removable discontinuity (a hole in the graph of the function) or a non-removable discontinuity (such as a jump or an asymptote in the graph):
-
If the function factors and the bottom term cancels, the discontinuity at the x-value for which the denominator was zero is removable, so the graph has a hole in it.
For example, this function factors as shown:
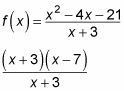
After canceling, it leaves you with x – 7. Therefore x + 3 = 0 (or x = –3) is a removable discontinuity — the graph has a hole, as you see in Figure A.
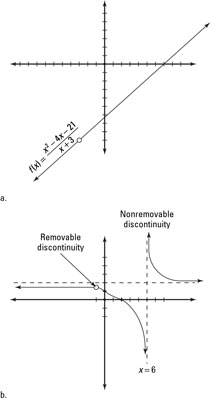The graph of removable leaves you feeling empty, whereas a graph of a non-removable discontinuity leaves you feeling jumpy. -
If a term doesn’t cancel, the discontinuity at this x value corresponding to this term for which the denominator is zero is nonremovable, and the graph has a vertical asymptote.
The following function factors as shown:
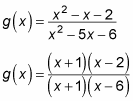
Because the x + 1 cancels, you have a removable at x = –1 (you’d see a hole in the graph there, not an asymptote). But the x – 6 didn’t cancel in the denominator, so you have a non-removable discontinuity at x = 6. This discontinuity creates a vertical asymptote in the graph at x = 6. Figure b shows the graph of g(x).
What Is A Removable Discontinuity
A removable discontinuity can be created by defining a blip in the graph like this.
 |
The above function tells us that the graph generally follows the function f(x)=x^2-1 except for at the point x=4. When we graph it, we will need to draw a little open circle at the point on the graph and mark that it equals 2 at that point. This is a created discontinuity. If you were the one defining the function, you can easily remove the discontinuity by redefining the function. Looking at the function f(x)=x^2-1, we can calculate that at x=4, f(x)=15. So, if we redefine our point at x=4 to equal 15, we will have removed our
 |
If we were to graph the above, we would get a continuous graph without any discontinuities. When you see functions written out like that, be sure to check whether the function really has a discontinuity or not. Sometimes the function is continuous but just written like it isn’t just to be tricky.
Give An Example Of A Function With Both A Removable And A Non-removable Discontinuity
A real-valued univariate function 
is said to have a removable discontinuity at a point 
in its domain provided that both 
and
 |
(1)
|
exist while 
. Removable discontinuities are so named because one can “remove” this point of discontinuity by defining an almost everywhere identical function 
of the form
 |
(2)
|
which necessarily is everywhere-continuous.
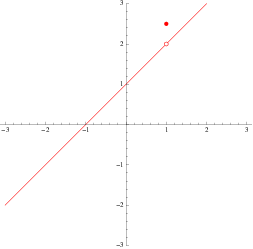
The figure above shows the piecewise function
 |
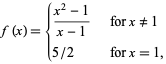(3)
|
A function for which 
while 
. In particular, 
has a removable discontinuity at 
due to the fact that defining a function 
as discussed above and satisfying 
would yield an everywhere-continuous version of 
.
Note that the given definition of removable discontinuity fails to apply to functions 
for which 
and for which 
fails to exist; in particular, the above definition allows one only to talk about a function being discontinuous at points for which it is defined. This definition isn’t uniform, however, and as a result, some authors claim that, e.g., 
has a removable discontinuity at the point 
. This notion is related to the so-called sinc function.
How Do You Know if A Discontinuity Is Removable?
A discontinuity is said to be removable if it can be fixed by redefining the value of the function at that point. Here are the steps to determine if a discontinuity is removable:
- Check if the function is defined at the point of discontinuity. If the function is not defined at the point, then the discontinuity is not removable.
- Check the limit of the function at the point of discontinuity. If the limit exists and is finite, then the discontinuity is removable.
- Compare the limit of the function at the point of discontinuity to the value of the function at that point. If the limit and value are different, then the discontinuity is removable.
- Check if the function can be factored so that the common factor cancels out with the denominator at the point of discontinuity. If this is the case, then the discontinuity is removable.
If all of these conditions are met, then the discontinuity is removable. In other words, the hole in the graph can be filled by redefining the value of the function at the point of discontinuity, creating a continuous function. If any of these conditions are not met, then the discontinuity is not removable and represents a true break in the function.
What Is The Equation For A Removable Discontinuity?
A removable discontinuity does not have a specific equation since it refers to a feature of a function’s graph rather than the function itself.
However, a function that has a removable discontinuity can be expressed as two separate functions, one that describes the part of the function before the hole, and another that describes the part of the function after the hole.
For example, consider the function f(x) = (x^2 – 4)/(x – 2). This function has a removable discontinuity at x = 2. To fill in the hole, you can redefine the function as:
f(x) = (x + 2) for x ≠ 2 f(2) = 4
This new definition creates a continuous function with no holes or breaks, and it is equivalent to the original function everywhere except at x = 2.
Read Also: How Much Does A Gallon Of Water Weigh?
Applications of Removable Discontinuity in Real-World Scenarios
Removable discontinuities are a fascinating and essential concept in mathematical analysis. They often appear in real-world scenarios and have practical applications across various domains. This article will explore some of the real-life situations where removable discontinuities are encountered and their significance in understanding and solving problems.
1. Physics and Engineering
In physics and engineering, removable discontinuities may arise in scenarios where a physical quantity changes abruptly due to a change in the conditions or constraints of a system. For example, consider a system where a mass is suspended on a spring. When the mass is suddenly removed, the spring’s force may exhibit a removable discontinuity. By redefining the force at the point of discontinuity, we can create a continuous function that accurately describes the system’s behavior. This aids in modeling and analyzing the system effectively.
2. Economics
In economics, removable discontinuities can be found in cost functions or production functions. For instance, a company’s production function may exhibit a removable discontinuity when the production of a certain quantity of goods is temporarily halted due to an external factor, such as a power outage. By redefining the function at the point of discontinuity, economists can create a continuous function that captures the company’s production capabilities more accurately. This helps in making more informed decisions about resource allocation, pricing, and market strategy.
3. Environmental Science
In environmental science, removable discontinuities may occur in data collected from various sources, such as temperature or air quality measurements. These discontinuities could result from faulty equipment, human error, or other factors that cause a sudden and temporary deviation in the data. By identifying and addressing the removable discontinuity, scientists can obtain a more accurate representation of the data, allowing for better analysis and understanding of environmental patterns and trends.
4. Medical Science
Removable discontinuities may appear in medical research, especially when analyzing data collected over time from patients or test subjects. These discontinuities could arise due to incomplete or incorrect data entry, sensor errors, or other factors that cause a temporary deviation from the expected results. By identifying the removable discontinuity and redefining the function at that point, medical researchers can obtain a more accurate representation of the data, which is crucial for drawing reliable conclusions and making informed decisions about patient care or treatment plans.
5. Computer Science and Data Analysis
In computer science and data analysis, removable discontinuities may arise when working with large datasets that contain errors or inconsistencies. For example, a dataset may have missing values or incorrect entries at certain points. Analysts can create a continuous function that provides a more accurate representation of the data, allowing for better insights and more reliable predictions.
In conclusion, removable discontinuities play a crucial role in various real-world applications. By identifying and addressing these discontinuities, professionals across different domains can create more accurate models and make better-informed decisions. Understanding the concept of removable discontinuity and its significance is essential for students to grasp its applications in real-life scenarios and to solve complex problems that involve discontinuous functions.
