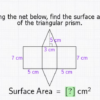
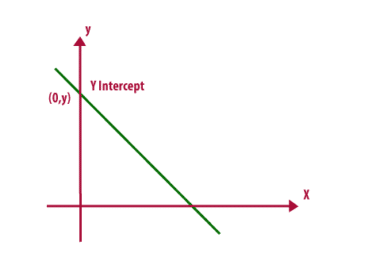
Finding the vertex of a parabola can be a daunting task, especially if you are not familiar with the n-th root of the parabola. There are several ways to do it, however. One of the most common methods is by using the Domain of a quadratic function, the y-intercept, and the x-intercept.
Different Ways to Find the y-intercept
There are different ways to find the y-intercept of a parabola. One method involves finding the x-intercept of a line. Another way uses the slope of the graph. You may also use the equation of a quadratic function to find the y-intercept.
The y-intercept of a parabola is the y-value that corresponds to a x-value when x = 0. It is found when you solve for y. In some cases, you can simply substitute the x-value into the equation and then find the y-intercept. This method is useful for problems where you have two points on a straight line. However, in many situations, you will need to solve for both x and y to find the y-intercept.
A quadratic equation has three main forms: standard, factored, and slope-intercept. In general, a quadratic equation can be written as y=ax + bx+c. In the standard form, ax and bx are known constants, and c is the y-intercept. Standard form is also called the vertex form.
Slope-intercept form is a type of equation in which y-intercept is a constant. It is also a type of equation where c is a constant. It is important to note that when a quadratic equation is written in a vertex form, it always has a vertex. This is the point at which the maximum or minimum value of the function occurs. If the y-intercept is replaced with a zero, the vertex will be at the opposite end of the graph.
Finding the y-intercept of a graph
Finding the y-intercept of a graph is not as hard as you might think. There are three basic techniques to do this. Firstly, you can use a table to identify the values of x and y. Secondly, you can find the y-coordinates of the vertex by dividing the x-coordinates. Lastly, you can calculate the difference between x-coordinates to find the slope.
When a quadratic equation is written in vertex form, the vertex is the lowest point on the graph. The vertex can be found by using a table, coordinates, or run and rise. For example, the vertex is at the bottom of the graph and occurs at x=-1/2. This makes a vertical line x = -2 the axis of symmetry.
To find the y-intercept of n graphs, it is necessary to solve for y. If you know the values of a, b, and c, then you can easily solve for y. However, if you do not know the values of a, b, or c, then you will need to solve for x.
As you can see, the y-intercept is the y-value that is found when x = 0 or the x-coordinate is minus one. It is not always possible to calculate the y-intercept of a line, but you can always determine the x-coordinate of the vertex.
Domain of a quadratic function
A parabola is a type of curve, akin to a U-shaped graph. Parabolas have a minimum or maximum value at a certain point on the graph. The lowest point on the graph is called the vertex, and is the turning point of the curve. To find the vertex of a quadratic function, you can use a general or standard form of the function. If you’re not sure which of the two forms is appropriate, consider the structure of the function and the range of the function.
In terms of quadratic functions, the vertex is usually found at the bottom of a “U” shape. It doesn’t have to be the origin, but it should be located along the axis of symmetry. This axis is the vertical line passing through the vertex.
The domain is the set of all the x values for which the function exists. These x values are all real numbers. For example, the domain of a square is all x values between 0 and 2. Similarly, the domain of a quadratic function is all x values from 0 to 2 and -2.875.
An equation for a quadratic function is y = ax2+bx+c, where a, b, and c are the constants. Usually, these are the standard forms of the quadratic function, but the domain can be written in other forms. Some of the common ways of presenting this type of equation include verbal, symbolic, and even a graph. All of these formats are helpful in solving algebraic problems.
Signs on the coordinates of the vertex
The vertex of a parabola is a point where the parabola passes the axis of symmetry. The vertex of a parabola can be found by calculating the x coordinate of the function. For this, we can use the binomial formula. This formula is a special form of quadratic equation.
It works in the following way: when you take the quadratic function and subtract the right number, you are given the x-coordinate of the vertex. If you add the right number to the x-coordinate, you are also given the y-coordinate of the vertex. A positive value for “H” will give the lowest point on the graph and a negative value will give the highest. However, if the graph contains an x-intercept, then the “H” value can be negative.
The axis of symmetry is the axis that divides the parabola into two parts. In this case, the axis of symmetry is the line FA. There are other pole-polar relationships, which are used in hyperbolas. These can be seen in the figure below.
Read Also: About Acostarse Reflexive Conjugation
When the sign of the a and y terms are positive, the parabola opens upward. On the other hand, if the sign of the a and y term is negative, the parabola will open downward. Also, the x-intercepts of the function can be used to calculate the x-coordinate of the vertex.
If the graph is graphed using x-intercepts, then the axis of symmetry is not included in the graph. Using the axis of symmetry is similar to using affine transformations. To find the x-coordinate of the vertex of a parabola, it is necessary to determine the distance between the axis of symmetry and the axis of the parabola.
The distance between the axis of symmetry of a parabola and the axis of the function is called the focus. The focus is the same point as the focus of the FC, the midpoint of the FC, and the point F.