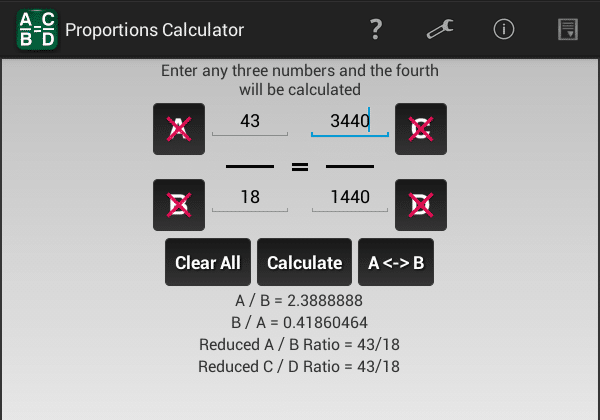
How to use the Proportion Calculator?
A Percentage Calculator is a free online tool that presents a percentage of a given expression. The internet percentage calculator tool makes the computations quicker and easier where it shows the percentage in a fraction of secs.
How to Utilize a Proportion Calculator?
Fix for an unidentified worth with this portions calculator. Find the missing out on portion variable in the percentage using cross multiplication to determine the unknown variable. Solve the rate between 2 fractions and calculate the missing out on fraction variable inequalities.
Get in 3 values and one unknown. For instance, go into 45= 115. The percentage calculator fixes for.
Exactly how to Address for x in Fractions
Solve for by cross multiplying and simplifying the equation to locate x.
Example: Provided the formula 410= 15 address for.
Cross increase the fractions.
4 × 15= 10 ×.
Resolve the equation for.
=( 4 × 15) 10.
Simplify for.
= 6.
To examine the job placed the outcome, six back into the initial formula.
410= 615.
Cross increase the fractions, and also you obtain.
4 × 15= 10 × 6.
60= 60.
Since 60= 60 holds, you can ensure that= 6 is the correct solution.
A portion with an absolutely no is undefined.
A portion with absolutely no numerator equals 0.
Percentage Calculator.
Why Does the Cross Multiplication Calculator for Portions Job?
Cross increasing works because you’re simply increasing both sides of the equation by 1. Since multiplying anything by one does t alter its value, you’ll have a comparable equation.
For instance, consider this equation.
=.
You obtain if you increase both sides by 1 using the denominators from the opposite of the equation.
×= ×.
Note that this does t modify anything since multiplying anything by one does t alter its worth. So now you have.
× ×= × ×.
Since the denominators are likewise the same right here, b × d, you can remove them and claim that.
×= ×.
This is the outcome of cross multiplying the “true” equation.
=.
Percentage.
Proportion is clarified majorly based upon balance and portions. A fraction stands for in the form of, while proportion specifies that two ratios are equivalent. Right here, and are any two integers. The balance, as well as a percentage, are essential structures to recognize the different ideas in mathematics as well as in science.
Proportion discovers application in fixing lots of day-to-day live troubles such as in-service while managing purchases or while food preparation, and so on. It develops a relation between 2 or more quantities and hence assists in their comparison.
What is Percentage?
Proportion, in general, is described as a component, share, or number taken into consideration in comparative relation to a whole. The percentage definition says that when two ratios are equivalent, they are in proportion. It is a formula or statement to depict that two proportions or fractions are equal.
Definition.
The percentage is a mathematical contrast between two numbers. According to proportion, if two collections of offered numbers are boosting or lowering in the same ratio, the ratios are stated to be straight symmetrical per other. Percentages are signified utilizing the symbol.
::=.
Instance.
Two proportions are said to be in proportion when both ratios are equivalent. For example, the time taken by train to cover 50 is equal to the moment it carries to cover the range of 250 5. Such as 50/= 250 5.
Proceeded Proportions
Any three quantities are claimed to be in continued percentage if the ratio between the first and the second amounts to the balance between the second and the 3rd. Similarly, four quantities in constant proportion will undoubtedly have the ratio between the initial and 2nd equal to the balance between the third and 4th.
For example, consider two ratios: a: b and c:d. To locate the ongoing percentage for both given ratio terms, we will undoubtedly convert their means to a solitary term/number. Typically, it would be the LCM of methods, and also, for the given ratio, the LCM of b & c will certainly be bc. Thus, multiplying the very first ratio by c and the 2nd ratio by b, we have
The first ratio-:.
The second ratio-:.
Hence, write the ongoing percentage for the given ratios in::.
Ratios and Percentages.
The ratio is a way of corresponding two portions of the identical kind by utilising division. Multiply and split each regard to a percentage by the same number (non-zero), which does t impact the ratio.
When two or more such ratios are equivalent, they are said to be in proportion.
Fourth, 3rd and also Mean Symmetrical.
If:=: after that:
It is called the fourth symmetrical too.
It is called the third proportional to and also.
The mean proportion between and also is ().
Tips and Tricks on Percentage and Using Proportion Calculator
Suppose both the numbers an and b are multiplied or divided by the same number in the ratio. In that case, the resulting ratio continues to be the same as the original ratio.
Percentage Solution with Examples.
Ratio Formula.
Think that we have any two quantities (or two entities), and we need to discover the ratio of these two. After that, the formula for ratio is specified as, where.
And also could be any two quantities.
It is called the initial term or antecedent.
It is called the 2nd term or following.
Ratio Formula.
Ratio Formula.
For example, in ratio 5:9, it stands for by 59, where 5 is antecedent and nine is consequent. 5:9= 10:18= 15:27.
Proportion Solution.
Currently, let us presume that, in proportion, both ratios are: and. The two terms are called, whereas the terms are referred to as extremes or extreme terms. Proportion Solution (Proportion Calculator). For example, allow us to take into consideration an additional instance of the variety of trainees in 2
The ratio of the number of ladies to young boys is equal. Our first ratio of the number of women to young lads is 2:5, and another is 4:8, then the percentage.
Kinds of Percentages
Based on the kind of relationship two or even more quantities share, the Percentage can be categorized into different types. There are two types of proportions.
Straight Proportion
Inverse Proportion
Types Of Proportion
Straight Proportion
This kind describes the direct partnership in between 2 quantities. In essential words, if one quantity boosts, the other various amount also increases and also vice-versa. For instance, if the rate of an automobile increases, it covers a lot more range in taking care of the quantity of time. In notation, the direct Percentage is composed as y ∝ x.
Inverse Proportion
This kind explains the indirect connection between two quantities. In short, words, if one quantity increases, the other quantity declines and vice-versa. In notation, an inverted proportion is created as y ∝ 1/x. As an example, raising the speed of the auto will result in covering taken care of distance in less time.
Distinction Between Ratio and Percentage and using Proportion Calculator
Proportion, as well as Percentage, are carefully relevant principles. The Percentage represents the equal partnership between two or even more ratios. To recognize the concept of Ratio and Percentage, undergo the distinction between Ratio and Percentage given here.
The Ratio contrasts the size of two things with the very same device. The Percentage is used to reveal the relationship of the two proportions.
It is expressed utilizing a colon (:-RRB- or reduce (/). It is described using the double colon (::-RRB- or equal to the sign (=-RRB-.
And, it is an expression. It is an equation.
The search phrase to differentiate proportion in a problem is “to every”. The keyword phrase to determine the Percentage in trouble is “out of”.
Important Notes on Proportion Calculator
Proportion is a mathematical contrast between 2 numbers.
Fundamental percentages are of two types: direct proportions and inverse proportions.
We can apply the principles of percentages to location, comparing amounts in physics, dietetics, cooking, etc.
Percentage establishes equivalent relation in between two ratios. The residential properties of Percentage that is complied with by this connection:
Proportion Calculator
- Alternendo – If 𝑎:𝑏=𝑐:𝑑, then 𝑎:𝑐=𝑏:𝑑
- Invertendo – If 𝑎:𝑏=𝑐:𝑑, then 𝑏:𝑎=𝑑:𝑐
- Componendo and dividendo – If 𝑎:𝑏=𝑐:𝑑, then 𝑎+𝑏:𝑎–𝑏=𝑐+𝑑:𝑐–𝑑
- Subtrahendo – If 𝑎:𝑏=𝑐:𝑑, then value of each ratio is 𝑎–𝑐:𝑏–𝑑
- Addendo – If 𝑎:𝑏=𝑐:𝑑, then value of each ratio is 𝑎+𝑐:𝑏+𝑑
- Componendo – If 𝑎:𝑏=𝑐:𝑑, then 𝑎+𝑏:𝑏=𝑐+𝑑:𝑑
- Dividendo – If 𝑎:𝑏=𝑐:𝑑, then 𝑎–𝑏:𝑏=𝑐–𝑑:𝑑